 |
| aturan sinus dan cosinus |
Tahukah kalian apa perbedaan antara aturan sinus dan aturan cosinus??
Secara sederhana, jika kalian menemukan soal yang mengharuskan pengerjaan dengan menggunakan aturan sinus dan aturan cosinus cukup dengan melihat dari soal yang diketahui. Misalnya ada sebuah segitiga diketahui dua sudut dan satu sisi atau dua sisi dan satu sudut bukan sudut apit, maka kalian dapat melakukan pengerjaan dengan mengggunakan aturan sinus. Sedangkan aturan cosinus digunakan ketika diketahui ketiga sisi atau dua sisi dan satu sudut apitnya.
ATURAN SINUS
Perhatikan segitiga ABC berikut ini.
 |
| segitiga ABC |
Setiap segitiga memiliki tiga sudut dan tiga sisi. Misalkan panjang sisi AB = c, BC = a dan AC = b. Sementara itu, besar sudut BAC = α, sudut ABC = ß dan sudut ACB = ɣ.
Jika diketahui panjang sisi a, panjang sisi b dan sudut α, bagaimana cara menentukan besar sudut ß? Jika diketahui besar sudut α dan ß, serta panjang sisi a, bagaimana cara menentukan panjang b?
Jadi untuk menyelesaikan permasalahan tersebut, kalian dapat menggunakan aturan sinus karena diketahui dua sudut dan satu sisi atau dua sisi dan satu sudut bukan sudut apit.
Untuk lebih jelasnya memahami rumus aturan sinus, kalian dapat melihat penjelasan berikut. Perhatikan kembali gambar.
- CD merupakan garis tinggi segitiga ABC terhadap sisi AB, jadi :
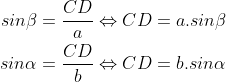
Dari kedua pernyataan tersebut, diperoleh :
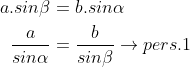
AE merupakan garis tinggi segitiga ABC terhadap sisi BC.
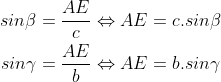
Dari kedua pernyataan diperolah:
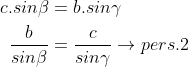
Dari persamaan 1 dan persamaan 2, diperoleh rumus aturan sinus sebagai berikut:
Contoh Soal 1
Diketahui segitiga ABC dengan besar sudut A = 30°, sudut B = 45° dan panjang sisi b = 12 cm, tentukan panjang sisi a.
Jawaban:
Untuk menjawab soal tersebut, coba kalian perhatikan gambar segitiga ABC berikut.
 |
| segitiga ABC |
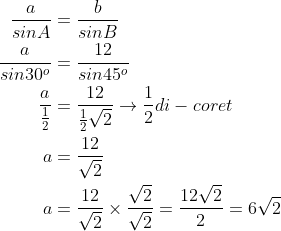
Jadi panjang sisi a = 6√2 cm.
Perhatikan bamgar segitiga ABC berikut ini.
 |
| segitiga ABC |
Tentukan besar sudut ABC.
Jawaban:
Dari gambar diatas, diketahui bahwa b = 8 cm, a = 4√6 cm dan besar sudut CAB = 60°.
Dengan menggunakan aturan sinus, dapat ditentukan besar sudut B dengan aturan sinus.
Jadi besar sudut ABC = 45° (sin yang bernilai 1/2 √2 adalah 45° )
Berbeda dengan aturan sinus, bahwa aturan cosinus digunakan untuk menghitung besaran lain dalam segitiga yang diketahui ketiga sisi atau dua sisi dan satu sudut apitnya.
Misalkan kalian mempunyai segitiga sembarang ABC yang diketahui ukuran sebuah sudut dan dua sisi yang mengapitnya dapat menggunakan aturan cosinus dalam proses perhitungan. Perhatikan gambar segitiga ABC berikut:
 |
| aturan cosinus |
Pada segitiga BCP, berlaku theorema phytagoras:
CB2
= CP2 + BP2 ….. persamaan. 1
Pada segitiga ACP diperoleh:
Langkah selanjutnya, coba kalian substitusikan persamaan 2 dan persamaan 3 ke dalam persamaan 1.
Sehingga diperoleh : a2
= b2 + c2 - 2bc.cosA
Dengan cara yang sama, teman-teman dapat memperoleh rumus aturan cosinus lain yaitu:
Aturan cosinus tersebut dapat dapat diubah menjadi bentuk berikut.
Contoh Soal 3
Diketahui segitiga ABC dengan panjang sisi a = 7 cm, c = 5 cm dan besar sudut B = 60°. Tentukan panjang sisi b.
Jawaban :
Untuk pengerjaan soal tersebut, kalian coba untuk membuat sketsa gambar terlebih dahulu seperti nampak gambar berikut.
 |
| segitiga ABC |
Jika kalian perhatikan segitiga ABC tersebut, sudut B merupakan sudut apit antara sisi a dan c. Aturan sinus tidak dapat digunakan untuk menentukan penyelesaian soal tersebut karena yang diketahui adalah sudut apit. Untuk menyelesaiakannya dapat digunakan aturan cosinus.
Dari pengerjaan diatas, dapat ditentukan bahwa panjang sisi b adalah √39 cm.
Contoh Soal 4
Diketahui segitiga PQR seperti berikut.
 |
| segitiga PQR |
Jika diketahui panjang p =
2√5 cm, q = 4√2
cm dan r = 6 cm. Tentukan besar sudut QPR
Jawaban :
Besar sudut QPR atau sudut P dapat dicari dengan menggunakan aturan cosinus.
Jadi besar sudut P adalah 45°
Contoh Soal 5
Dua kapal laut berselancar secara bersilangan dengan sudut 60°. Pada saat tertentu kapal pertama berada 10 km dari titik silang dan kapal kedua 16 km dari titik silang. Jarak kedua kapal laut tersebut pada saat itu adalah ...
A. 12 km
B. 14 km
C. 16 km
D. 18 km
E. 20 km
Jawaban:
Terlebih dahulu kalian gambar yang menunjukkan keadaan tersebut.
 |
| aturan cosinus |
Jika kalian perhatikan gambar tersebut, jelas bahwa ada dua sisi dan satu sudut apit yang diketahui. Maka untuk menentukan jarak kapal 1 dengan kapal 2 digunakan aturan cosinus.
Jadi jarak kapal 1 terhadap kapal 2 adalah 14 km.
Demikian materi tentang aturan sinus dan aturan cosinus, semoga dapat bermanfaat bagi kalian semua. Sukses selalu dan tetap semangat.










Post a Comment for "Aturan Sinus dan Cosinus"