Perbandingan Trigonometri Sudut Siku-siku
 |
| perbandingan trigonometri |
Tahukah teman-teman bahwa untuk menghitung ketinggian sebuah rumah, gedung, pohon, bahkan ketinggian gunung dapat memanfaatkan ilmu trigonometri?? Jadi teman-teman tidak perlu repot-repot menggunakan penggaris untuk mengukur ketinggian sebuah benda yang sangat tinggi dan tidak dapat kita jangkau. Bagaimana caranya?? Simak penjelasan berikut ini ya ...
Untuk menentukan ketinggian sebuah benda, teman-teman dapat menggunakan yang namanya perbandingan trigonometri. Kali ini, kita akan bersama-sama belajar mengenai perbandingan trigonometri. Ada dua perbandingan trigonometri yaitu perbandingan trigonometri dalam segitiga siku-siku dan perbandingan trigonometri sudut-sudut istimewa.
Baca juga : Pengukuran Sudut
PERBANDINGAN TRIGONOMETRI SEGITIGA SIKU-SIKU
Perhatikan gambar berikut:
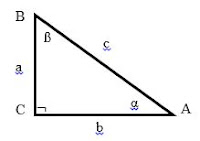 |
| segitiga ABC siku-siku di C |
Segitiga ABC merupakan segitiga siku-siku di C dengan panjang sisi AB = c, AC = b dan BC = a serta besar sudut BAC = α , sudut ABC = ß dan sudut ACB = 90°.
Teman-teman tentu masih ingat dengan theorema phytagoras bahwa:
Berdasarkan gambar segitiga ABC diatas, dapat didefinisikan bahwa perbandingan panjang sisi-sisi segitiga berikut.
Jika teman-teman melihat perbandingan untuk sudut α, maka :
BC = a = sisi depan (de)
AC = b = sisi samping (sa)
AB = c = sisi miring (mi)
Tetapi jika teman-teman melihat perbandingan untuk sudut ß maka:
BC = a = sisi samping (sa)
AC = b = sisi depan (de)
AB = c = sisi miring (mi)
Selain perbandingan trigonometri tersebut, masih ada 3 perbandingan trigonometri yang lain yaitu :
Untuk rumusnya, teman-teman dapat membuatnya sendiri ya tinggal di balik saja penempatannya.
Contoh soal 1
Perhatikan gambar berikut
 |
| gb.2 |
a. sin α
b. cos ß
c. tan α
d. cosec α
e. sec ß
Jawaban
Seperti yang diketahui dalam gambar diatas bahwa :
AB = 5 cm, AC = 4 cm
Sebelumnya teman-teman harus mencari panjang dari BC dengan menggunakan teorema phytagoras.
Untuk teman-teman perhatikan bahwa, jika kita akan menghitung perbandingan trigonometri sudut α maka sisi AC = samping, BC = depan dan AB = miring sedangkan jika kita akan menghitung perbandingan trigonometri sudut ß maka sisi AC = depan, BC = samping, AB = miring.
Demikian pembahasan untuk perbandingan trigonometri dalam segitiga siku-siku. Sangat mudah untuk dipahami bukan? Semoga kalian bisa paham dan memahami.
PERBANDINGAN TRIGONOMETRI SUDUT-SUDUT ISTIMEWA
Sudut-sudut istimewa adalah sudut yang besarnya 0°, 30°, 45°, 60°, dan 90°. Untuk lebih jelasnya teman-teman dapat melihat tabel berikut.
Contoh Soal 1
Diketahui ∆ ABC siku-siku di C. JIka panjang sisi BC = 20 cm dan besar sudut BAC = 30° , tentukan panjang sisi AB dan AC.
Jawaban
Langkah pertama teman-teman coba untuk membuat sketsa gambarnya terlebih dahulu seperti berikut.
Kemudian analisis bahwa sisi AC = samping, BC = depan, dan AB = miring. Jadi untuk menentukan panjang AB teman-teman dapat menggunakan perbandingan sin 30° seperti berikut.
Untuk menentukan panjang AC, teman-teman punya 2 cara. Cara pertama dengan menggunakan theorema phytagoras, dan cara kedua dengan menggunakan perbandingan trigonometri sudut tan.
Cara 1 (theorema phytagoras)
Cara 2 (perbandingan trigonometri tan)
Jadi panjang AC = 20√3 cm.
Contoh soal 2
Budi melihat puncak pohon dengan sudut 30° terhadap garis horizontal dari jarak 6 meter. Tentuakn tinggi pohon jika tinggi Budi adalah 1,6 meter seperti nampak pada gambar berikut.
Jawaban
Dari gambar diatas, jika kita gambarkan dalam segitiga yang lebih sederhana akan menjadi :
 |
| gb. segitiga ABC |
AC = sisi samping
BC = sisi depan
Jadi perbandingan yang dapat dipakai adalah tan.
Jadi ketinggian pohon tersebut adalah 2√3 + tinggi Budi = (2√3 + 1,6) meter
Baca Juga : Pengukuran Sudut




Post a Comment for "Perbandingan Trigonometri Sudut Siku-siku"