INVERS MATRIKS
 |
Kemarin kita sudah belajar banyak hal mengenai matriks ya mulai jenis matriks, operasi matriks, transpose sampai dengan determinan matriks. Lalu bagaimana dengan invers matriks ? Sama halnya dengan determinan matriks, invers juga akan kita pelajari untuk yang berordo 2x2 dan 3x3. Bagaimana caranya?? simak penjelasan berikut..
Invers Matriks Ordo 2x2
Invers dari sebuah matriks disimbolkan dengan 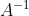 . Misalkan kalian punya matriks
. Misalkan kalian punya matriks 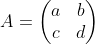 . Untuk mencari nilai inversnya, jika dapat menggunakan rumus :
. Untuk mencari nilai inversnya, jika dapat menggunakan rumus :
Contoh
Jawab:
Dari soal tersebut kita tahu bahwa nilai a = 3, b = -5 , c = 4 dan d = - 7
Untuk menentukan invers matriks A diatas, terlebih dahulu kita mencari determinan dari matriks A. JIka sudah lupa silakan baca kembali determinan matriks ordo 2x2.
|A| = [3.(-7)] - [(-5).4] = - 21 - (-20) = - 21 + 20 = - 1
Setelah kita tahu nilai determinan, selanjutnya kita baru mencari inversnya.
Bagaimana, mudah bukan? sering-latihan supaya kalian lebih paham dengan materi ini. Setelah kalian paham dengan materi ini, kita dapat melanjutkan untuk menghitung invers matriks ordo 3x3.
Invers Matriks Ordo 3x3
Berbeda dengan ordo 2x2, invers matriks ordo 3x3 mungkin lebih panjang penyelesaiannya, tapi tidak masalah yang penting ada niat dan usaha pasti bisa.
Untuk menentukan invers matriks ordo 3x3 kita gunakan cara adjoin, apa itu?
Rumus untuk mencari invers matriks ordo 3x3 adalah :
dengan |A| ≠ 0
Perhatikan contoh
Tentukan invers dari matriks berikut
Jawab
Langkah pertama kita cari dulu determinan matriks A. Jika kalian lupa silakan baca kembali determinan matriks ordo 3x3
Setelah kita cari determinan matriks A, selanjutnya hitung kofaktor dari elemen matriks A, dengan rumus ^{i+j}.m^{ij}) dengan i adalah baris sedangkan j adalah kolom.
dengan i adalah baris sedangkan j adalah kolom.
m-ij adalah minor matriks A pada baris i kolom j (minor = menghilangkan/mengeliminasi)
Misal : m-11 artinya eliminasi baris 1 kolom 1 , m-23 artinya eliminasi baris 2 kolom 3 dari elemen matriks A kemudian tulis sisanya elemen yang tidak di eliminasi dalam sebuah determinan. Selanjutnya hitung determinan dari elminasi tersebut dengan mengalikan silang (lihat kembali determinan ordo 2x2)
Selanjutnya, hitung kofaktornya dari setiap elemen matriks A
Catatan : i artinya baris, j artinya kolom
Setelah kita menghitung kofaktor, langkah selanjutnya adalah menuliskan dalam matriks kofaktor A
Setelah itu, kita tulis adjoin dari matrks A dengan cara menentukan transpose dari kofaktor matriks A
dengan menggunakan adjoin matriks, dapat kita tentukan invers dari matriks A sebagai berikut :
OK teman-teman, invers matriks ordo 2x2 dan ordo 3x3 sudah dapat kita pelajari. Kelihatan susah ya untuk matriks ordo 3x3, tetapi jika kalian mau berlatih dan sunguh-sungguh pasti akan bisa kok, tetap semangat ...

Post a Comment for "INVERS MATRIKS"